APPROACHES AND STRATEGIES IN TEACHING AND LEARNING OF MATHEMATICS

APPROACHES AND STRATEGIES IN TEACHING AND LEARNING OF MATHEMATICS

 Five E model

It is a process in which the teacher plans structured activities or creates learning environments, implements them in classrooms, guides students to construct the knowledge or discover the knowledge through this activities and gives feedback for further progress or improvement in learning.

   The structured activities or learning environment are planned based on various methods and techniques depending on the purpose for which they are designed. The present trend is to plan the learning environments based on some Instructional design model.

Instructional design model.

       An Instructional design is a decision making process by means of which the most appropriate instructional strategy is selected to achieve an identified objective under a set of conditions. Instructional design requires development of learning material using learning theories and instructional strategies to ensure quality of design, delivery and effectiveness of transfer of learning to intended outcomes.

     It provides wider scope for teachers to plan and create learning environments and facilitate learning. Within the broad frame work of the instructional design, the teacher wisely selects and organizes suitable methods and strategies depending on the content category and the objectives to be achieved. It also involves assessment and evaluation strategies.

The various questions answered by the instructional design are presented in the following diagram.

The recommendation made by NCF 2005 is that the mode of transaction should be through constructivism. Hence, instructional design models constructivism are to be followed. There are several instructional design models based constructivism and one of the suitable model for science and mathematics subjects and most often used model is Five E’s model developed by Roger Bybee.

Five E’s Model Stage

State-1: Engage: 

This stage assess the previous knowledge of the learner and helps them become engaged in a new concept through the use of short activities that promote curiosity and elicit prior knowledge. The aim is to organize students’ thinking toward the learning outcomes of the current activities.

        Facilitating learning environment, learning activities and situations and focusing the minds of learners on the higher order learning tasks is the main purpose of this stage. As far as possible present real life situations to engage student’s attention on learning tasks.

The different ways of engaging learners are:

·         Ask open ended questions.

·         Act out a problematic situation.

·         Define a problem.

·         Show a surprising event.

·         Note unexpected phenomenon.

·         Consider possible responses to questions.

·         Present situations where student’s perceptions vary.

Stage-2: Explore:

In this stage, learners are guided to explore and find answers for the questions/issues raised during the engage stage. Teacher role is to structure and present learning environment which facilitate learners to involve in investigative activities and provide opportunities for students to get directly involved with discovery process and construction of knowledge.

     Expose the students to a variety of experiences at this stage. These experiences may involve observations of events or objects, manipulations of materials, work with simulations, examinations of representations, viewing a short video, or reading. These experiences provide a common basis for all students that the teacher can use the assist them in identifying and developing concepts and skills.

     Some of the investigative activities can be as follows:

·         Provide structured activities.

·         Have them work in teams.

·         Experiment with materials.

·         Use their inquiry to drive the process.

·         Employ problem solving strategies.

·         Identify sequence or patterns of events.

·         Brainstorm possible alternatives.

According to constructivist approaches, it is very suitable to structure small groups

(3 to 6 members) while involving students in the above mentioned activities or any appropriate activity. Co-operative learning strategies are most suitable for this purpose.

Stage-3: Explain:

Here students are provided with opportunity to explain their understanding of their experiences from the explore phase. The questions and discussion lead students to patterns, regularities, and/or similarities and prompt them to describe concepts or skills in their own words.

At the second stage, students have engaged in the learning activities and through mutual interactions discovered the knowledge (scientific facts, concepts, generalizations and procedures) and constructed. Expressing this abstract knowledge through communicable form is the purpose of the third stage.

Students can express the constructed knowledge in different ways as follows:

·         Explain the constructed ideas.

·         Construct and explain a model.

·         Represent ideas through pictures/figures/graphs.

·         Represent information through symbols.

·         Present a summary based on the data.

·         Present oral and written reports.

·         Review and criticize solutions.

Stage-4: Expand/Elaborate:

    This phase challenges students to extend their understandings or skills and/or to practicae them. Through new experiences at this time, students develop deeper understanding, an extended conceptural framework, and improved skills. Some of the tasks, such as reading an article, may be done as homework and discussed during the following class period.

In the fourth stage, the teacher provides opportunities and guidance for students to apply the constructed knowledge in several real life situations. The students can also correlate the newly constructed knowledge to other related fields of knowledge. These new relationships can further lead to new discoveries or new understandings.

·         Apply knowledge and skills in real life situations.

·         Transfer knowledge and skills.

·         Ask new questions.

Stage-5: Evaluate:

 The final phase of the instructional model encourages students to assess their understanding and abilities and provides opportunity for the teacher to evaluate student progress toward achieving the learning objectives for the activity. The tasks may involve writing summaries, applying concepts and skills to novel situations, constructing a concept map. Or taking a quiz.

At this stage the teacher evaluates whether the students have constructed the knowledge completely and correctly and also have developed conceptual understandings. According to constructivist theory, evaluation should be as far as possible diagnostic in nature.

The tools that are suitable for this purpose are:

·         Checklists for observations.

·         Projects and problem based learning products.

·         Achievement and attainment tests.

·         Concept/mind mappings.

·         Portfolios assessments.

·         Rubrics.

·         Student interviews

Example:

Subject: Geometry                                                                        Class: IX

Topic: Length of segment parallel to either X or Y axis.

Technique: 5 E Model

1.ENGAGE	Show pieces of straws to the class and ask them how they can find the length of the same. Obviously they will want to use a measuring scale. Ask them for methods to find the length of a straw without using a measuring scale. Ask them for methods to find the length of a straw without using a measuring scale. Show them diferent types of paper as plain paper, graph paper, craft paper and see if the length of the straws can be measured. Apparently a graph paper comes in handy. That is because there is a relationship between the co-ordinates of points and the length of the segment determined by two such points. Here the teacher announces that the class is going to discover this relationship to find the length of a segment.
2.EXPLORE	Have points and their co-ordinates put up on the chalkboard as follows:  Group I :i) A (3,6) B (5,6) ii) T (5,8) V (1,8) Group II: i) X (7,14) Y (7,10) ii) M (3,2) N (3,8) Is there any common characteristics of each group? Where would the pair D (8, 8) and E (8,4) go? Students are encouraged to plot one pair on their graph papers. All students of Group I compare their segments and derive one common property. The same is done by Group II. Can the length of the segment be found out? Is there a relationship between the co-ordinates of the endpoints and the length of the segment?
3. EXPLAIN	The students are encouraged to explain this relationship in their own words. On the basis of their work they devise a formula to find the length of the segment parallel to X asis. Similarly find the length of the segment parallel to y axis.
4. ELABORATE	Where will this formula be useful? Here the teacher can probe for an answer.
5. EVALUATE	Give each Student a card with co-ordinates of a point. Students pair up and try to find the length of the segment formed. Be sure that the co-ordinates are such that the segment formed must be parallel to one of the two axes. Pair up with a different student and now find the length of the new segment.

The students devise the formula on their own. They get adequate practice through the game. The teacher only facilitates through use of appropriate questions.

APPROACHES AND MODELS OF TEACHING MATHEMATICS

Inducto-Deductive approach:         

INDUCTIVE METHOD

     Inductive method is advocated by Pestalozzi and Francis Bacon. Inductive method is based on induction. Induction is the process of proving a universal truth or a theorem by showing that if it is true of any particular case, it is true of the next case in the same serial order and hence true for any such cases. Thus it is a method of arriving at a formula or a rule by observing a sufficient number of particular instances. If one rule applies to a particular case and is equally applicable to different similar cases, it is accepted as a general rule or formula. Therefore, inductive method proceeds from,

i)                    Particular cases to general rules or formulae.

ii)                   Concrete instance to abstract rules.

iii)                 Known to unknown.

iv)                 Simple to complex.

        This method has been found to be very suitable for the teaching of mathematics because many mathematical formulae and generalizations are the results of induction.

For example: If we wish to frame the formula (a-b)² =a² – 2ab + b². Let the students actually multiply

(a-b) x (a-b) and find out the product. They may then be asked to find the answers for (p-q)², (l-m)² etc. by actually multiplication. After this they be asked to observe results and be helped to make generalization to get the required formula.

Steps in Inductive Method

1.       Selection of a number of cases.

2.       Observation of the case under given conditions.

3.       Investigation and analysis.

4.       Finding common relations.

5.       Arriving at generalization.

6.       Verification or application.

Example-1:

If two parallel lines are cut by a transversal the alternate angles are equal.

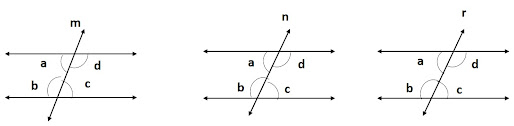
Step-1: Selection of a number of cases:

      Students may be asked to draw  at least three pairs of parallel lines cut by transversal and mark the pair of alternate angles as a, b ,c, d.                                                                                                                                   

                                                                                                                                                                                                    

    The Students can be asked to measure the angles a, b, c, and d, and tabulate the results.

Step-2: Observation of the cases under given conditions:

By appropriate questioning the students may be asked to observe the cases and see the common property and similarity of the given instances i.e.

i)                    A pair of parallel lines cut by a transversal

ii)                   ∟a and ∟c  (a pair of alternate angles)

∟b and ∟d   (a pair of alternate angles)

Step-3: Investigation and analysis for common properties and relations.

     The students are asked to analyse the data tabulated by them and draw inferences regarding common properties

Cases	m ∟a	m ∟b	m ∟c	m ∟d
Case-(i)	60	42	60	42
Case-(ii)	55	60	55	60
Case-(iii)	45	75	45	75

Step-4: Finding common relations:

 From the tabulated data it can be observed that

m∟a= m ∟c

m∟b= m ∟d

Step-5: Arriving at generalization:

a = c (a and c are alternate angles)

b = d (b and d are alternate angles)

        . ^.. Alternate angles are equal i.e. when two parallel lines are cut by a transversal, the alternate angles are equal.

Step-6: Verification or application:

       Require the students to verify the validity of the generalization by applying it to a new situation.

Merits of Inductive method

1.       It helps in understanding.

2.       It is logical method and develops critical thinking.

3.       It encourages active participation of the students in learning.

4.       It provides ample opportunities for exploration and observation.

5.       It sustains the students’ interest as they proceed from known to unknown.

6.       It curbs the tendency to rote learning as it clears the doubts of the students.

7.       It facilitates meaningful learning.

8.       It enhances self-confidence.

9.       It is helpful for beginners as it provides a number of concrete examples.

10.   It encourages experimentation, observation, analytical thinking and reasoning.

11.   It facilitates fixation and retention of mathematical concepts, rules and formulae.

12.   It helps in increasing the pupil-teacher contact.

13.   It does not burden the mind. Formula becomes easy to remember.

14.   It discourages cramming and also reduces home work.

Demerits of Inductive method

1.       This method is limited in range and is not suitable for all topics. Certain complex and complicated formula cannot be generalized in this manner.

2.       It is lengthy, time consuming and laborious method.

3.       Inductive reasoning is not absolutely conclusive because the generalization made with the help of a few specific examples may not holds good in all cases.

4.       We don’t complete the study of a topic simply by discovering a formula but a lot of supplementary work and practice is required for fixing the topic in learner’s mind.

5.       This method is not suitable for higher classes because higher order mathematical principles cannot be generalized through the observation of concrete cases.

6.       It is not suitable for mathematically gifted students as unnecessary details and too many examples make the teaching dull and boring.

Applicability of Inductive method

Inductive method is most suitable where

·         Rules are to be formulated.

·         Definitions are to be formulated.

·         Formulae are to be derived.

·         Generalizations or laws are to be arrived at.

DEDUCTIVE METHOD

        Deductive method is based on deductive reasoning. Deductive reasoning is the process of drawing logical inferences from established facts or fundamental assumptions. Contrary to inductive method, in deductive method we begin with the formula, or rule or generalization and apply it to a particular case. In this method, the teacher presents the known facts or generalization and draws inferences regarding the unknown, following a network of reasoning. Therefore, deductive method proceeds from:

i)                    General rule to specific instances.

ii)                   Unknown rule to known case.

iii)                 Abstract rule to concrete instance.

iv)                 Complex rule to simple example.

            Example: the formula.          Simple interest = Principal X rate X time

100

Steps in Deductive method

Deductive method of teaching follows the steps given below for effective teaching.

1.       Clear recognition of the problem: A clear recognition of the problem statement provides the basic link for the thinking process and the solution to the problem.

2.       Search for a tentative hypothesis: The second step in deductive method is the search for tentative hypothesis, a tentative solution to the problem.

3.       Formulation of tentative hypothesis: The search for the solution leads to the formulation of a tentative hypothesis that appears to have promise as a possible or probable solution to the problem. The tentative hypothesis has its basis on certain axioms or postulates, or propositions or rules and formulae that have been accepted to be true.

4.       Verification: Finally the hypothesis that has been formulated is to be verified as the right solution to the problem at hand.

Example: Find the area of an equilateral triangle of side 3 cm.

Step-1: Clear recognition of problem.

      The student analyses the problem as to what is given and what is to be found out.

          Given:  An equilateral triangle of side 3 cm.

            Problem: To find its area.

Step-2: Search for tentative hypothesis:

     The student analyses various possible solutions i.e. various formulae for the area of triangle that they have encountered before such as, A=½ b h; A = ½ a b

             A = √s(s-a)s(s-b)s(s-c), A = √3/4   a²

Step-3: Formulation of tentative hypothesis:

     The student select A =√3/4   a² as a possible hypothesis as it is the formula to find the area of an equilateral triangle.

Step-4: Verification:

      The student verifies the hypothesis

         A =√3/4   a² Sq. unit

         A =√3/4 x  3²

     i.e.    A =√3/4 x 9 Sq.cm

Deductive method is very frequently followed by teachers of mathematics, as mathematics is a deductive science. Problems can be solved by applying formulae and rules that have been already derived. Theorems and riders can be deducted from theorems which have been already proved, definitions that have been stated and postulates and axioms that have been accepted.

Differences between Inductive and Deductive methods:

INDUCTIVE METHOD	DEDUCTIVE METHOD
1. In this method we proceed from ‘particular to general’, from example to general rule’, and from ‘concrete to abstract’.	1. In this method, we proceed from general to particular, from general to rule to example and from abstract to concrete.
2. In this method, Child acts as researcher and draws law or formula by active participation.	2. In this formulae and laws are already told to the child. He is not able to verify the law or formula.
3. By this method, a habit of discovery is developed in students.	3. By this method, a habit of discovery is not developed in students.
4. This is best method of teaching.	4. This is best method of learning.
5. Inductive method is suitable for teaching in lower classes.	5. This method is suitable for teaching in higher classes.
6. In this method, children themselves decide the law or formula. It develops self-reliance and self-confidence in them.	6. In this method laws and formulae are told in advance so they do not gain any confidence.
7. This method is helpful in discovering new knowledge.	7. In this method children use the knowledge gained by others.
8. This is a scientific method by which scientific attitude is developed in students.	8. This method does not give any scope for developing scientific attitude in children.
9. This method is the way of discovery and research.	9. This method is the way of following because child follow the given laws and principles.
10. In this method, both the teacher and pupils are active. So this is a student-centered method.	10. In this, teacher is more active and pupil is a passive learner.so this is a teacher-centered method.
11. This method give emphasis on original and creative work.	11. This method gives emphasis on problem-solving.
12. Teaching-learning process becomes interesting by the use of this method.	12. Teaching-learning process becomes dull by the use of this method.
13. In this method, every step is important to write so many steps.	13. In this method children do not learn and children learn to write them.
14. This is a slow method, so it needs more labour and time.	14. This is a fast method so it needs less labour and times.
15. This is a psychological method which is understanding centered.	15. This is an unpsychological method and is memory-centered.

ANALYTIC METHOD

            The word ‘analytic’ is derived from the word ‘analysis’ which means ‘breaking up’ or resolving a thing into its constituent elements. This method is based on analysis and therefore in this method we break up the problem in hand into its constituent parts so that it ultimately gets connected with something obvious, or already known. In this process we start with what is to be found out (unknown) and then think of further steps and possibilities which may connect with the known and find out the desired result. Hence in this method we proceed from unknown to known, from abstract to concrete and from complex to simple. This method is particularly useful for solving problems in arithmetic, algebra, geometry and trigonometry.

Example: If a/b = c/d prove that ac + 3b² = c² + 3bd

bc               dc

                To prove this using analytic method, begin from the unknown.

                The unknown is   ac + 3b² = c² + 3bd

bc               dc

ac + 3b² = c² + 3bd is true

bc               dc

ifac + 3b² = c² + 3bdis true

b              d

if   d (ac+3b²) = b (c² + 3b²d)

dac + 3db²= bc² + 3db²

ifdac = bc²

if da = bc

if a/b = c/d which is given to be  true.

∴ac + 3b² = c² + 3bd

bc               dc

In analysis the reasoning is as follows:

       ‘C’ is true if ‘B’ is true

      ‘B’ is true if ‘A’ is true

∴ ‘C’ is true

Merits of Analytic Method

1.       It leaves no doubts in the minds of the students as every step is justified.

2.       It is a psychological method.

3.       It facilitates clear understanding of the subject matter as every step is derived by the student himself.

4.       It helps in developing the spirit of enquiry and discovery among the students.

5.       No cramming is necessitated in this method as each step has its reason and justification.

6.       Students take active role in the learning process resulting in longer retention and easier recall of what they learn.

7.       It develops self-confidence in the students as they tackle the problems confidently and intelligently.

8.       It develops thinking and reasoning power among the students.

Demerits of Analytic Method

1.       It is a lengthy, time consuming method and therefore not economical.

2.       With this method it is difficult to acquire efficiency and speed.

3.       This method may not be suitable for all topics of mathematics.

4.       In this method information is not presented in a well-organized manner.

5.       This method may not be very effective for below average students who would find it difficult to follow the analytical reasoning.

Applicability of Analytic Method

     Analytic Method, though it has got certain limitations, is very effective for teaching how to solve complex mathematical problems, in proving theorems and riders and teaching many topics from algebra.  This method is particularly useful for solving problems in arithmetic, algebra, geometry and trigonometry.

SYNTHETIC METHOD

      ‘Synthetic’ is derived from the word ‘Synthesis’. Synthesis is the complement of analysis. To synthesise is to combine the constituent elements to produce something new. In this method we start with something already known and connect it with the unknown part of the statement. Therefore, in this method one proceed from known to unknown. It is the process of combining known bits of information to reach the point where unknown information becomes obvious and true. In synthetic method the reasoning is as follows “Since A is true, B is true”.

      The usual forms of statements of proofs found in textbook are examples of synthetic method. Beginning with known definitions, assumptions and axioms, the sequence of steps are deducted and conclusions (unknown) are arrived at.

     Synthetic method is best suited for the final presentation of proofs of theorems and solutions to problems in a logical and systematic manner. However, it is advisable to adopt synthetic method following analytic method.

Example:     If a/b = c/d ,  prove that ac + 3b² = c² + 3bd

bc               dc

                 In synthetic method, one has to begin with the known i.e. a/b = c/d and reach the unknown i.e. ac + 3b² = c² + 3bd

bc               dc

Proof: a/b = c/d (known)

Adding 3b/c on both sides we get

a/b + 3b/c  = c/d + 3b/c

ac + 3b² = c2 + 3bd

bc             dc

Thus beginning with the known, the unknown is reached. But why +3b/c   is added is not explained.

  In synthetic method the reasoning is as follows.

A is true.

∴ B is true and

∴ C is true

Merits of Synthetic Method

1.       This method is logical as in this method one proceeds from the known to unknown.

2.       It is short and elegant.

3.       It facilitates speed and efficiency.

4.       It is more effective for slow learners.

Demerits of Synthetic method

1.       It leaves many doubts in the minds of the learner and offers no explanations for them.

2.       As it does not justify all the steps, recall of all the steps may not be possible.

3.       There is no scope for discovery and enquiry in this method.

4.       It makes the students passive listeners and encourage rote memorization.

5.       If the students forget the sequence of steps, it could be very difficult to reconstruct the proof/Solutions.

Application of Synthetic method

     Synthetic method is best suited for the final presentation of proofs of theorems and solutions to problems in a logical and systematic manner. Many teachers prefer this method for teaching mathematics. However it is advisable to adopt synthetic method following analytical method.

Differences between Analytic and Synthetic methods:

ANALYTIC METHOD	SYNTHETIC METHOD
1. We proceed from unknown to known or from conclusion to hypothesis.	1. We proceed from known to unknown or hypothesis to conclusion.
2. It is based on inductive reasoning.	2. It is based on deductive reasoning.
3. It is based upon heuristic approach.	3. It is not based on heuristic approach.
4. It is laborious and very lengthy method.	4. It is short and quick method.
5. It helps in the development of self-confidence and self-reliance.	5. No development of self-reliance and Self-confidence. With the help of this method.
6. Helps in the development of intellectual abilities.	6. It does not help in the developments of intellectual abilities.
7. It is psychological in nature.	7. It is unpsychological in nature.
8. Approach is scientific in nature.	8. Approach is unscientific in nature.
9. It is a formative method.	9. It is an informative method.
10. It develops originality and creativity with reasoning.	10. More stress on memory of the child without reasoning.
11. This method leads in the discovery of something new.	11. This method does not lead on the discovery of something new
12. Subject matter becomes solid and durable for a longer time.	12. It is time being and the content is not durable for a longer time.
13. Proof can be easily recollected if forgotten.	13. Once forgotten proof cannot be recollected.
14. It is process of thinking.	14. It is product of thinking.
15. Close contact between the teacher and the taught.	15. No such intimate contact between them.

GUIDED DISCOVERY APPROACH

Guided discovery has emerged as a valuable strategy of teaching mathematics. In teaching, the teacher exercises some guidance over the learner’s behaviour. If this guidance is limited, them guided discovery can take place. In this strategy of teaching, the pupils is encouraged to think for himself and to discover general principles from situations, which may be contrived by the teacher if necessary.

     True discovery teaching is a process, which focuses on the learner. The pupils have a tendency to jump conclusions quickly to generalize on a very limited data, moreover how many students are sufficiently brilliant to discover everything they are to know in mathematics.

     Bruner says discovery is a process, a way of approaching problems rather than the product of the knowledge. It is his contentions that process of discovery can become generalized abilities though exercise of solving problems and the practice.

     Basically it is a process that presents mathematics in a way that makes some sense to the learner. It is an instructional process in which the learner is placed in a situation where he is free to explore, manipulate materials, investigate and concluded. The teacher assumes the role as a guide. He helps the learner to draw upon ideas, concepts and skills that have already been learnt in order to conclude new knowledge asking appropriate questions will do a great deal to encourage the situation.

Principles or Steps of Guided Discovery:

1.      Motivation: Psychologist believe that almost all children have a built in will to learn. It is desired to know the external world. It is the basic for human learning.   Motivation can be done in variety though proper questions, solving problems, through examples, through using visual aids, methods, charts, etc.

2.      Structure: It states that any body of knowledge can be organized in such a way that almost every student can understand it. The form of knowledge, which is presented to the children, can be made simple that a learner understands it is a recognized form.

At this stage of thinking the message of the teacher should be through movements, actions, and experience. At symbolic level children can translate experiences into language. Level of thinking makes use of pictures and diagrams, which allow the children to be learnt in simple ways. Anything that is easily understood is the powerful presentation. New relationship can be established between facts through powerful presentation.

3.      Sequence:The lesson should follow sequential arrangement of the subject matter. Usually we start with the diagrams and pictorial representation to symbolic communication. The teacher can explain or present the matter through diagrams and pictures and explain the very content of them.

4.      Reinforcement: In order to achieve mastery over the knowledge, we should get feedback. The pupils are made to use the acquired knowledge in different situations, so that they learn better and by practice understanding of the subject will be better.

Types of lessons inGuided discovery method:

1.       Concept formation lessons.

2.       Concept utilization lessons.

3.       MarticeTenon lessons.

4.       Concept enrichment lesson.

CONCEPT ATTAINMENT MODEL

Concept Attainment

Concept attainment is an indirect instructional strategy that uses a structured inquiry process. It is based on the work of Jerome Bruner. In concept attainment, students figure out the attributes of a group or category that has already been formed by the teacher. To do so, students compare and contrast examples that contain the attribute. They then separate them into two groups. Concept attainment, then, is the search for and identification of attributes that can be used to distinguish examples of a given group or category from non-examples.

Purpose of Concept attainment model

     Concept attainment is designed to clarify ideas and to introduce aspects of content. It engages students into formulating a concept through the use of illustrations, word cards or specimens called examples. Students who catch onto the idea before others are able to resolve the concept and then are invited to suggest their own examples, while other students are still trying to form the concept. For their reason, concept attainment is well suited to classroom use because all thinking abilities can be changed throughout the activity. With carefully chosen examples, it is possible to use concept attainment to teach almost any concept in all subjects.

Syntax of concept attainment model:

Phase-I: Presentation of data and identification of concept:

This involves presentation of data to learners. Each unit of data is a separate example or non-example of the concept. The data may be events, people, objects, stories, pictures or any other discriminable units. The learners are informed that there is one idea that all the positive examples have in common, their task is to develop a hypothesis about the nature of the concept. The instances are presented in a prearranged order and are labeled ‘yes’ or ‘no’. Learners are asked to compare and justify the attributes of different examples. Finally, they are asked to name their concepts and state the rules or definitions of the concepts according to their essential attributes.

Phase-II: Testing Attainment of the concept:

     The students test their attainment of the concept, first by correctly identifying additional unlabeled examples of the concept and then by generating their own examples. After this the teacher (and students) confirm or disconfirm their original hypothesis, revising their choice of concepts or attributes as necessary.

Phase-III: Analysis of thinking strategies:

Students begin to analyse the strategies by which they attain concepts. As we have indicated, some learners initially try broad constructs and gradually narrow the field, other begin with more discrete constructs. The learners can describe their patterns, whether they focused on attributes or concepts, whether they did so one at a time or several at once.

Steps of Concept Attainment:

1.  Select and define a concept.

2.  Select the attributes.

3. Develop positive and negative examples.

4. Introduce the process to the students.

5. Present the example and list the attributes.

6. Develop a concept definition.

7. Give additional examples.

8. Discuss the process with the class.

9. Evaluate.

A Mathematical example:

1.       First the teacher chooses a concept to develop. (i.e., Math facts that equal to 10).

2.       Begin by making list of both positive “yes” and negative “no” examples. The examples are put on to sheets of paper or flash cards.

3.       Positive examples:(Positive examples contain attributes of the concept to be taught) i.e.,  5+5, 11-1, 10x1, 3+4+4, (4x2) +2, 12-2, 15-5, 9+1,

4.       Negative examples: (for examples choose facts that do not have 10 as the answer) i.e., 6+6,

 3 +3, 12-4, 3 x3, 4x4, 16 -5, 6x2, 3+4+6, 2+ (2x3), 16-10,

5.       Designate one area of the chalkboard for the positive examples and one area for negative examples. A chart could be set up at the front of the room with two columns-one marked YES and the other marked with NO.

6.       Present the first card by saying, “This is a YES.” Place it under the appropriate column.i.e. 5+5 is YES.

7.       Present the next card and say, “This is NO.” Place it under the NO column. i.e.6+6 is a NO.

8.       Repeat this process until there are three examples under each column.

9.       Ask the class to look at the three examples under the YES column and discuss how they are alike (i.e.,5+5,11-1, 2x5, ) Ask “What do they have in common?”.

10.    For the next three examples under each column. Several students will have identified the concept but it is important that they not tell it out loud to the class. They can however show that they have caught on by giving an example of their own for each column. At this point, the examples are student-generated. Ask the class if anyone else has the concept in mind. Students who have not yet defined the concept are still busy trying to see the similarities of the YES examples. Place at least three more examples under each column that are student-generated.

11.    Discuss the process with the class. Once most students have caught on, they can define the concept. Once they have pointed out that everything under the YES column has an answer of 10, then print a new heading at the top of the column (10 facts). The print a new heading for the NO column (Not 10 facts).

How can we adapt it?

     This activity can be done on the chalkboard, chart paper or overhead projector to a large or small group. It also works well as one-on-work. Rather than starting with the teacher’s concept, use a student’s concept. Concept attainment can be used to introduce or conclude unit of study.

Variations on the Concept Attainment Model

1.       Present all of the positive examples to the students at once and have them determine the essential attributes.

2.       Present all of the positive and negative examples to the students without labeling them as such. Have them group the examples into the two categories and determine the essential attributes.

3.       Have the students define, identify the essential attributes of, and choose positive examples for a concept already learned in class.

4.       Use the model as a group activity.

Assessment and Evaluation Considerations

Have the students:

1.       Write the definition from memory.

2.       Determine positive and negative examples from a given group.

3.       Create their own examples of the concept.

4.       “Think aloud”.

5.       Write a learning log.

6.       Do an oral presentation.

7.       Create a web, concept map, flow chart, illustrations, KWL chart, T chart.

Advantages:

1.       Helps to make connections between what students know and what they will be learning.

2.       Learn how to examine a concept from a number of perspectives.

3.       Learn how to sort out relevant information.

4.       Extends their knowledge of a concept by classifying more than one example of that concept.

5.       Students go beyond merely associating a key term with a definition.

6.       Concept is learned more thoroughly and retention is improved.