Axioms,Postulates,Theorems

Axioms

      While proving any statement logically, we have to depend on theorems, postulates and axioms for reasoning. It is impossible to establish logical proofs without using the mathematical axioms and geometrical postulates.

Definition of Axiom                                                                              

·          

·         Axioms are certain elementary statements, the truth which are accepted without discussion and proof are called axioms. Some of the axioms are applicable to all the branches f mathematics.

Axiom-1: Things which are equal to the same thing are equal to one another.

Example-1: Observe the figures given and compare the lengths of the segments AB and CD. o

                                 AB = CD = 5cm…………. (1)          A   ________5cm________________   B

                        Compare the lengths AB and XY       C    __________5cm_______________   D

                                    AB= XY= 5cm………  (2)            X   ___________5cm_______________   Y

From (1) and (2)    AB = XY

Axiom-2: If equals are added to equals, the wholes are equal

Ex-1: If   a = b, then a+5 = b+5

Ex-2:

Here,

     ∟ABC = ∟MNP = 10⁰

      ∟CBD = ∟PNO = 20⁰

Adding       ∟ABC + ∟CBD = 10⁰+ 20⁰ = 30⁰   =   ∟ABD ……….. (1)

                     ∟MNP + ∟PNO = 10⁰+ 20⁰ = 30⁰   = ∟MNO ……… (2)

The facts from the above examples can be generalized.

Ex-2:

Here is an axiom of addition and multiplication.
Let x and y be real numbers.
Then x + y is also a real number and x y is also a real number

Solved Example on Axiom

Question: Which of the following is the basic axiom of algebra represented by the equation

3x + 7 = 7 + 3x, where x is any real number?
35, 45, 61, 59, 73

Choices:

Inverse property of addition
B. Associative property of addition
C. Identity property of addition
D. Commutative property of addition
Correct Answer: D

Solution:

Step 1: 3x + 7 = 7 + 3x, where x is any real number.
Step 2: It is of the form a + b = b + a.
Step 3: So, commutative property of addition is the basic axiom of algebra represented by the given equation.

 

Postulates

Postulates are the statements which specify relationships among basic geometric facts and concepts which are assumed to be true without logical proofs. Postulates are special axioms of geometry.

·         Postulate. A statement, also known as an axiom, which is taken to be true without proof.    

·         Postulates are the basic structure from which lemmas and theorems are derived. The whole of Euclidean geometry, for example, is based on five postulates known as Euclid's postulates.

·         Postulate definition. A statement accepted as true for the purposes of argument or scientific investigation; also, a basic principle.

Definition of Postulate

Postulate is a true statement, which does not require to be proved.

Postulate-1: One and only one straight line can be drawn through two points.

 

Postulate-2: Any number of lines can be drawn through a point.

 

Postulate-3: A straight line may be produced to any length on either side.

More about Postulate

Postulate is used to derive the other logical statements to solve a problem.
Postulates are also called as axioms.

Example of Postulate

To prove that these triangles are congruent, we use SSS postulate, as the corresponding sides of both the triangles are equal.

Solved Example on Postulate

Question: State the postulate or theorem you would use to prove that ∠1 and ∠2 are congruent.

Choices:

·         A. corresponding angles postulate

·         B. converse of corresponding angles postulate

·         C. alternate angles are congruent

·         D. adjacent angles are congruent

Correct Answer: A

Solution:

·         Step 1: ∠1 and ∠2 corresponding angles.

·         Step 2: Since the lines a and b are parallel, ∠1 and ∠2 are congruent. [Corresponding angles postulate.]

·         Step 3: So, corresponding angles postulate is used to prove that ∠1 and ∠2 are congruent.

What Is a Postulate?

A postulate is a statement that is accepted without proof. Axiom is another name for a postulate. For example, if you know that Pam is five feet tall and all her siblings are taller than her, you would believe her if she said that all of her siblings are at least five foot one. Pam just stated a postulate, and you just accepted it without grabbing a tape measure to verify the height of her siblings.

Conjectures are often confused with postulates. Conjectures are conclusions that we make based on things that we observe. For example, if from Sunday to Thursday, Sam usually had pancakes for breakfast, you'd be safe in assuming he'd have pancakes on Friday and Saturday. However, on Friday, Sam may just have oatmeal. While conjectures may need to be proven before they're accepted, postulates are givens and need no proof. Every mathematical theorem began as a conjecture or a postulate before they were tested and accepted as proven mathematical facts, such as the ones we'll explore below.

Examples: Operational Postulates

The following are some postulates that apply to the four operations, including addition, subtraction, multiplication, and division. These postulates are also algebraic properties used to solve algebraic equations.

The Addition Postulate: If you have one apple and Sally has one apple, when you both add the same quantity to your existing number of apples, you'll still have the same number of apples. Using algebra, the postulate states:

If x = y, then x + 4 = y + 4

The Subtraction Postulate: If you have ten apples and Sally has ten apples, when you both subtract the same quantity of apples from your existing number of apples, you'll still have the same number of apples.

If x = y, then x - 3 = y - 3

Without being repetitive, these same principles apply to both multiplication and division.

The Multiplication Postulate: If x = y, then x * 3 = y * 3

The Division Postulate: If x = y, then x / 7 = y / 7Support               Bottom of Form

Examples: Geometric Postulates

Geometric postulates can help us solve problems with lines, line segments, and angles. Let's see what they say.

The Ruler Postulate: Points on a line can match up with real numbers. In other words, each point on the line will represent a real number.

The Segment Addition Postulate: Remember that a segment has two endpoints. If you have a line segment with endpoints A and B, and point C is between points A and B, then AC + CB = AB.

The Angle Addition Postulate: This postulates states that if you divide one angle into two smaller angles, then the sum of those two angles must be equal to the measure of the original angle. Formally, if ray QS divides angle PQR, then the measure of the angles PQS, plus the measure of angle SQR, is equal to the measure of angle PQR.

The segment addition postulate and the angle addition postulate are called partition postulates. The idea behind partition postulates is this: if you cut your slice of bread into four pieces, when added together, those four pieces must form the whole slice. Similarly, if you divide a line or angle into two parts, then the sum of those two parts must be equal to the whole line or the whole angle.

Theorems

      A theorem is proposition in which some statement has to be proved logically. The statement itself is called the general enunciation (statements).

     The enunciation of a theorem consists of two parts. The first part is called hypothesis and states what is to be assumed. The second part is called the conclusion and states what is to be proved.

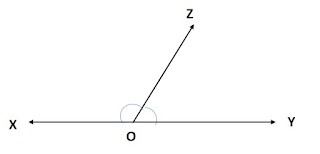
Example-1:

Enunciation: If a ray stands on a line, then the sum of adjacent angles formed is 180⁰.

                                                                               

                         Data: A ray stands on a straight line forming adjacent angles.

                         To prove: Sum of the adjacent angles is equal to 180⁰.

                             ∟XOZ +   ∟ZOY =   180⁰

Example-2:

Enunciation: If a transversal intersects two parallel line, then any pair of corresponding angles are equal.

                                                                                       

Date: Corresponding angles are formed when a transversal, intersects two parallel lines.

To prove: Corresponding angles are equal.

Converse of theorem:If two statements are such that the hypothesis of one is the conclusion of the other and vice-versa, then either of statements is said to be the converse of the other, converse of the statement given in example-2.

      If a transversal intersects two lines in such a way that a pair of corresponding angles are equal; then two lines are parallel,

Data:The transversal intersecting two straight lines, makes equal corresponding angles are equal, then the two lines are parallel.

To prove that: The two lines intersected by the transversal are paralleled.

Comparison of a statement and its converse:

Theorem	Converse of the Theorem
Enunciation: If a transversal intersects two parallel lines, then any pair of corresponding angles are equal.	If transversal intersects two lines in such a way that a pair of corresponding angles is equal, then the two lines are parallel.
Data: A transversal intersects two parallel lines.	A transversal intersects two lines in such a way that pair of corresponding angles, are equal.
To prove: To corresponding angles are equal.	The two lines are parallel.

     Therefore the hypothesis (data) of the theorem is the conclusion of the converse (to prove). The conclusion of the theorem (to prove) is the hypothesis (data) of the converse.

Steps to be followed while proving a theorem logically

1.       Read the statement of the theorem carefully.

2.       Identify the data and what is to be proved.

3.       Draw a rough diagram for a given data.

4.       Write the data and what is to be proved by using suitable symbols applicable to the figure drawn.

5.       Analyse the logical step to be followed in providing the theorem.

6.       Based on the analysis, if there is a need for any construction, do the necessary construction in the figure with the help of dotted line. Write the construction done symbolically under the step construction.

7.       Write the logical proof step by step by stating reasons for each step.

Converse, Inverse, Contrapositive

Given an if-then statement "if pp, then qq," we can create three related statements:

A conditional statement consists of two parts, a hypothesis in the “if” clause and a conclusion in the “then” clause.  For instance, “If it rains, then they cancel school.” 
              "It rains" is the hypothesis.
              "They cancel school" is the conclusion.

To form the converse of the conditional statement, interchange the hypothesis and the conclusion.
            The converse of "If it rains, then they cancel school" is "If they cancel school, then it rains."

To form the inverse of the conditional statement, take the negation of both the hypothesis and the conclusion.
            The inverse of “If it rains, then they cancel school” is “If it does not rain, then they do not cancel school.”

To form the contrapositive of the conditional statement, interchange the hypothesis and the conclusion of the inverse statement. 
            The contrapositive of "If it rains, then they cancel school" is "If they do not cancel school, then it does not rain."

Statement	If pp, then qq.
Converse	If qq, then pp.
Inverse	If not pp, then not qq.
Contrapositive	If not qq, then not pp.

If the statement is true, then the contrapositive is also logically true. If the converse is true, then the inverse is also logically true.

Example 1:

Statement	If two angles are congruent, then they have the same measure.
Converse	If two angles have the same measure, then they are congruent.
Inverse	If two angles are not congruent, then they do not have the same measure.
Contrapositive	If two angles do not have the same measure, then they are not congruent.

In the above example, since the hypothesis and conclusion are equivalent, all four statements are true. But this will not always be the case!

Example 2:

Statement	If a quadrilateral is a rectangle, then it has two pairs of parallel sides.
Converse	If a quadrilateral has two pairs of parallel sides, then it is a rectangle. (FALSE!)
Inverse	If a quadrilateral is not a rectangle, then it does not have two pairs of parallel sides. (FALSE!)
Contrapositive	If a quadrilateral does not have two pairs of parallel sides, then it is not a rectangle.

PROOFS.

A proof of a theorem is a finite sequence of claims, each claim being derived logically (i.e. by substituting in some tautology) from the previous claims, as well as theorems whose truth has been already established. The last claim in the sequence is the statement of the theorem, or a statement that clearly implies the theorem. We wish now to give some examples that will illustrate how this works in practice, as well as some techniques of proofs.

Different types of proofs

1.     Direct proof

In direct proof, the conclusion is established by logically combining the axioms, definitions, and earlier theorems.For example, direct proof can be used to establish that the sum of two even integers is always even:

Consider two even integers x and y. Since they are even, they can be written as x = 2a and y = 2b, respectively, for integers a and b. Then the sum x + y = 2a + 2b = 2(a+b). Therefore x+y has 2 as a factor and, by definition, is even. Hence the sum of any two even integers is even.

This proof uses the definition of even integers, the integer properties of closure under addition and multiplication, and distributive.

2.     Proof by mathematical induction

Despite its name, mathematical induction is a method of deduction, not a form of inductive reasoning. In proof by mathematical induction, a single "base case" is proved, and an "induction rule" is proved that establishes that any arbitrary case implies the next case. Since in principle the induction rule can be applied repeatedly starting from the proved base case, we see that all (usually infinitely many) cases are provable.^[14] This avoids having to prove each case individually. A variant of mathematical induction is proof by infinite descent, which can be used, for example, to prove the irrationality of the square root of two.

A common application of proof by mathematical induction is to prove that a property known to hold for one number holds for all natural numbers:Let N = {1,2,3,4,...} be the set of natural numbers, and P(n) be a mathematical statement involving the natural number n belonging to N such that

·        (i) P (1) is true, i.e., P (n) is true for n = 1.

·        (ii) P (n+1) is true whenever P (n) is true, i.e., P (n) is true implies that P (n+1) is true.

·        Then P (n) is true for all natural numbers n.

For example, we can prove by induction that all positive integers of the form 2n − 1 are odd. Let 

P (n) represent "2n − 1 is odd":

(i) For n = 1, 2n − 1 = 2(1) − 1 = 1, and 1 is odd, since it leaves a remainder of 1 when divided by 2. Thus P(1) is true.

(ii) For any n, if 2n − 1 is odd (P(n)), then (2n − 1) + 2 must also be odd, because adding 2 to an odd number results in an odd number. But(2n − 1) + 2 = 2n + 1 = 2(n+1) − 1, so 2(n+1) − 1 is odd (P(n+1)). So P(n) implies P(n+1).

Thus 2n − 1 is odd, for all positive integers n.

The shorter phrase "proof by induction" is often used instead of "proof by mathematical induction".

3.       Proof by contraposition

Proof by contraposition infers the conclusion "if p then q" from the premise "if not q then not

p". The statement "if not q then not p" is called the contrapositive of the statement "ifp then q". For

example, contraposition can be used to establish that, given an integer x, if x² is even, then x is even:

Suppose x is not even. Then x is odd. The product of two odd numbers is odd, hence x² = x·x is odd. Thus x² is not even. Thus, if x² is even, the supposition must be false, sox has to be even.

4.     Proof by contradiction

In proof by contradiction (also known as reduction absurdum, Latin for "by reduction to the

absurd"), it is shown that if some statement were true, a logical contradiction occurs, hence the

Statement must be false. A famous example of proof by contradiction shows that {\displaystyle {\sqrt {2}}}is an 

Irrational number:

Suppose that {\displaystyle {\sqrt {2}}}were a rational number, so by definition {\displaystyle {\sqrt {2}}={a \over b}} where a and b are non-zero integers with no common factor. (If there is a common factor, divide both numerator and denominator by that factor to remove it, and repeat until no common factor remains. By the method of infinite descent, this process must terminate.) Thus,{\displaystyle b{\sqrt {2}}=a} Squaring both sides yields 2b² = a². Since 2 divides the left hand side, 2 must also divide the right hand side (otherwise an even number would equal an odd number). So a² is even, which implies that a must also be even. So we can write a = 2c, where c is also an integer. Substitution into the original equation yields 2b² = (2c)² = 4c². Dividing both sides by 2 yields b² = 2c². But then, by the same argument as before, 2 divides b², so b must be even. However, if a and b are both even, they have a common factor, namely 2. This contradicts our initial supposition, so we are forced to conclude that {\displaystyle {\sqrt {2}}} is an irrational number.

5.     Proof by construction

Proof by construction, or proof by example, is the construction of a concrete example with a property to show that something having that property exists. Joseph Liouville, for instance, proved the existence of transcendental numbers by constructing an explicit example. It can also be used to construct a counterexample to disprove a proposition that all elements have a certain property.

6.     Proof by exhaustion

In proof by exhaustion, the conclusion is established by dividing it into a finite number of cases and proving each one separately. The number of cases sometimes can become very large. For example, the first proof of the four color theorem was a proof by exhaustion with 1,936 cases. This proof was controversial because the majority of the cases were checked by a computer program, not by hand. The shortest known proof of the four color theorem as of 2011 still has over 600 cases.

7.     Probabilistic proof

A probabilistic proof is one in which an example is shown to exist, with certainty, by using methods of probability theory. Probabilistic proof, like proof by construction, is one of many ways to show existence theorems.

This is not to be confused with an argument that a theorem is 'probably' true, a 'plausibility

argument'. The work on the Collatz conjecture shows how far plausibility is from genuine proof.^[17]

8.     Combinatorial proof

A combinatorial proof establishes the equivalence of different expressions by showing that they count the same object in different ways. Often a bijection between two sets is used to show that the expressions for their two sizes are equal. Alternatively, a double counting argument provides two different expressions for the size of a single set, again showing that the two expressions are equal.

9.     Nonconstructive proof

A nonconstructive proof establishes that a mathematical object with a certain property exists without explaining how such an object can be found. Often, this takes the form of a proof by contradiction in which the nonexistence of the object is proved to be impossible. In contrast, a constructive proof establishes that a particular object exists by providing a method of finding it. A famous example of a nonconstructive proof shows that there exist two irrational numbers a and b such that {\displaystyle a^{b}}is a rational number:

Either {\displaystyle {\sqrt {2}}^{\sqrt {2}}} is a rational number and we are done (take{\displaystyle a=b={\sqrt {2}}}), or {\displaystyle {\sqrt {2}}^{\sqrt {2}}} is irrational so we can write {\displaystyle a={\sqrt {2}}^{\sqrt {2}}}and{\displaystyle b={\sqrt {2}}}. This then gives{\displaystyle \left({\sqrt {2}}^{\sqrt {2}}\right)^{\sqrt {2}}={\sqrt {2}}^{2}=2}, which is thus a rational of the form {\displaystyle a^{b}.}

10. Statistical proofs in pure mathematics

The expression "statistical proof" may be used technically or colloquially in areas of pure mathematics, such as involving cryptography, chaotic series, and probabilistic or analyticnumber theory.^[18][19][20] It is less commonly used to refer to a mathematical proof in the branch of mathematics known as mathematical statistics. See also "Statistical proof using data" section below.

11. Computer-assisted proofs

Until the twentieth century it was assumed that any proof could, in principle, be checked by a competent mathematician to confirm its validity.^[7] However, computers are now used both to prove theorems and to carry out calculations that are too long for any human or team of humans to check; the first proof of the four color theorem is an example of a computer-assisted proof. Some mathematicians are concerned that the possibility of an error in a computer program or a run-time error in its calculations calls the validity of such computer-assisted proofs into question. In practice, the chances of an error invalidating a computer-assisted proof can be reduced by incorporating redundancy and self-checks into calculations, and by developing multiple independent approaches and programs. Errors can never be completely ruled out in case of verification of a proof by humans either, especially if the proof contains natural language and requires deep mathematical insight.

12.    Proofs by construction

A proof by construction is one in which anobjectthat proves the truth value of an statement is built, or found There are two main uses of this technique:

 –Proofthat a statement with an existential

 –Proofthat a statement with an existential quantifier is true

 –And disproof by counterexample:  this is a proof that a statement with a universal quantifier, is false

Example: 1

Statement: “There is a prime number between 45 and 54”

Proof: Search for an object: we examine one by one, the numbers between 45 and 54, until a prime is found. If no prime were found, the statement would be false.

  Numbers                                                      is it prime?

45No,because it is divisible by 5

46No, because is divisible by 2

47Yes, 47 is divisibleonly by 1 and 47

Conclusion: the statement is true(no need to check the rest of the numbers from 48 to 54)

Example: 2

Statement: “Let m and n be integers. Then, there is no integer k such that

                                 (3m+2)(3n+2) = 3k+2